Hvis man klipper et stykke papir ud, og folder det til en kasse, får man et volume af en vis størrelse. I dette eksempel bruges et kvadratisk stykke papir, som så skal foldes på en måde, så det giver en kasse med det størst mulige volume. Der er flere måder man kan bruge til at finde den optimale løsning, prøv dem alle af:
Find ud af om der er forskel på volumens størrelse, afhængigt af hvor stort et hak man folder ind.
Denne metode er lidt besværlig, for man skal lave mindst 3 forsøg, før man ved om man er i nærheden af resultatet. Efter disse 3 forsøg, har man måske fundet den optimale løsning. Det er knap så effektivt, men det er et bedre resultat, end ikke noget resultat.
Print 3 stk af 12x12 kassen, og klip henholdsvis 1, 2 og 3 tern ind. Fold kasserne og gæt hvilken en af kasserne der indeholder flest terninger (har det største volume). Tæl eller mål hvor mange tern de indeholder, og skriv det på kasserne. Er volumen det samme for alle kasser, eller hvilken kasse har det største volume?
Se på kasserne, tæl ternene og tast ind på lommeregner.
| DXF | PS | |
|---|---|---|
| Opgave 1 | ||
| 12x12kasse.optimering.dxf.gz | 12x12kasse.optimering.pdf | 12x12kasse.optimering.ps |
| Opgave 2 | ||
| 7x8kasse.optimering.dxf.gz | 7x8kasse.optimering.pdf | 7x8kasse.optimering.ps |
 | Print ud |
 | Klip ét hak i hvert hjørne, fx 2x2 tern, bemærk den røde streg |
 | Fold 2x2 flapper ind |
 | Fold 8x2 flapper ind |
 | Sæt en hæfteklamme eller et stykke tape i hvert hjørne |
 | Sæt en hæfteklamme eller et stykke tape i hvert hjørne |
 | Regn ud: Den måler 8x8x2 |
Det er givet at papiret har 12x12 tern. Man kan nøjes med at bruge 10x12 tern, men det største volume fås ved at bruge alle tern. Volumen kan beregnes ved at gange de 3 sider med hinanden, fx hvis der klippes 1 tern: 1x10x10. Formlen for udregning kan generaliseres ved bruge variablen x, hvor x er det antal tern der klippes ind:
V = h * b * d
V = h * (12 - h - h) * (12 - h - h)
Og hvis vi så sætter h til 2, så bliver det:
V = 2 * (12 - 2 - 2) * (12 - 2 - 2)
V = 2 * (8) * (8) = 128
En nem måde at få tegnet en graf på, er ved at søge efter formlen i Googles søgemaskine. Søg efter x * (12 - x - x) * (12 - x - x) formlen og se dette resultat:
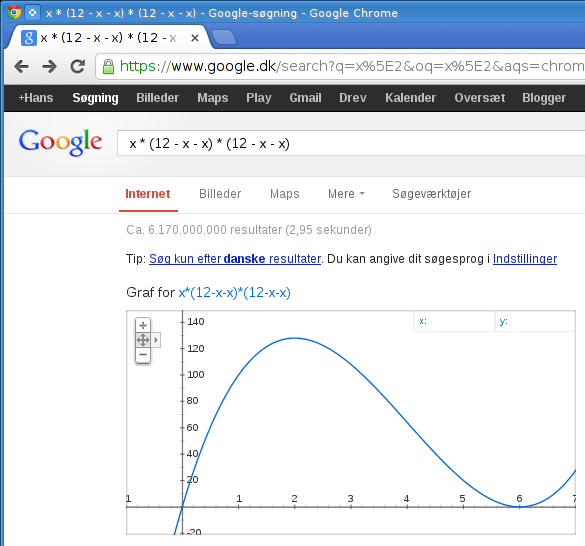
Flyt musen frem og tilbage over grafen, og aflæse toppunktet øverst i højre hjørne af grafen.
Søger man efter det reducerede udtryk kommer svaret lidt hurtigere, klik her: 4x^3 - 48x^2 + 144x
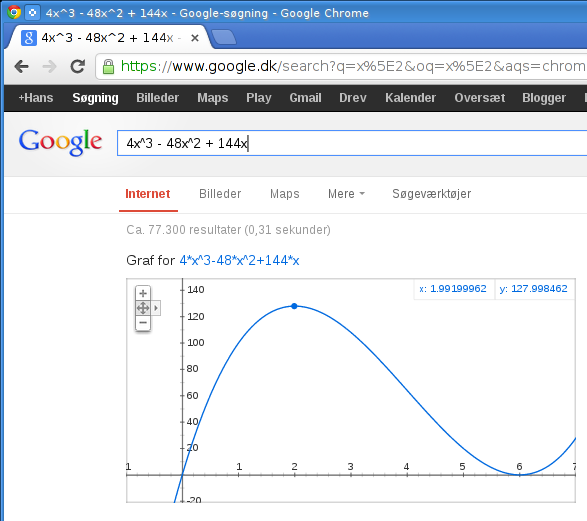
En nem måde at finde det optimale volume, er ved at prøve sig frem. Ved at bruge den simple ikke-reducerede formel h * (12-2*h) * (12-2*h), og taste den ind i et Google regneark som her, kan man nemt se hvor volume 'V' stiger og falder. Formlen ser lidt anderledes ud i regnearket, hvor 'h' er udskiftet med 'A6'. Det man så skal lægge mærke til, er hvor toppunktet af volume er, og det er så lige ved h=2 at volume er 128, og det er toppunktet. Ved at tegne en graf, bliver det helt tydeligt hvor toppunktet er.
Formlen for at regne volume ud er 'h*b*d', men da både 'b' og 'd' er afhængige af 'h', så skal vi bare have isoleret 'h', for så der kun er en variabel tilbage.
V = h * b * d
V = h * (12 - h - h) * (12 - h - h)
V = A6 * (12 - A6 - A6) * (12 - A6 - A6)
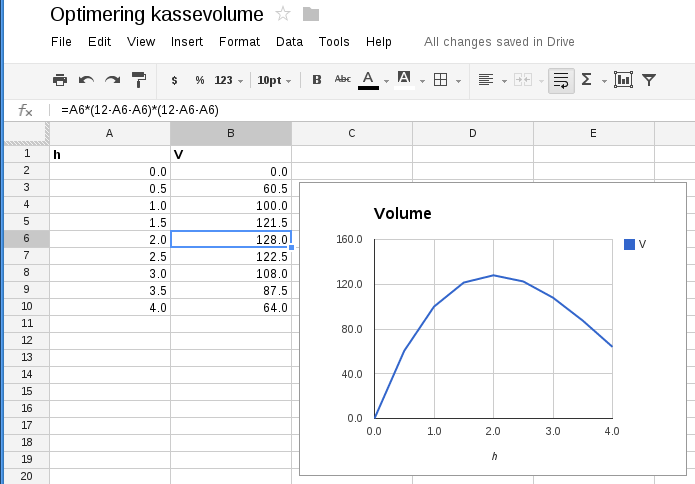
Nogle gange gange står man med en ligning, hvor det ikke er ligetil at løse ligningen og isolere x. Ved at lave et computerprogram, kan man så sætte computeren til at prøve alle mulige løsninger, indtil man får et tal der er præcist nok.
Metoden er at man først prøver med en lav værdi af x, hvor x er det antal tern man vil klippe. Dernæst lægger man lidt til med variablen step, og prøver og resultatet blev større, altså at det beregnede volumen blev større. Hvis resultatet bliver mindre end sidst, så er x kommet på den forkerte side af toppunktet, og vi gør så step halvt så stor og vender fortegnet så vi prøver med x den anden vej. Når forskellen mellem det nyligt beregnede volume v_2 og v_1 er mindre end 0.1, så siger vi at resultatet er tæt nok på, og vi stopper beregningen.
De to program eksempler herunder under gør præcist det samme, det er blot forskellige sprog.
#! /usr/bin/python #* #* af Hans Schou 2013 w = 12.0 d = 12.0 step = w / (2 * 4) x = 0.0 v_1 = -1.0 v_2 = 0.0 print "x\tV2\tV1\tstep" while ( v_2 - v_1 > 0.1 ): while ( v_2 > v_1 ): x = x + step v_1 = v_2 v_2 = x * (w - x - x) * (d - x - x) print "%.3lf\t%.2lf\t%.2lf\t%.4lf" % (x, v_2, v_1, step) step = step * -0.5 swap = v_2 v_2 = v_1 v_1 = swap
/*
* af Hans Schou 2013
*
* Kompilér og test:
* gcc -o kasseoptimeringnumerisk kasseoptimeringnumerisk.c && ./kasseoptimeringnumerisk
*/
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
int main(int argc, char *argv[]) {
double w = 12.0;
double d = 12.0;
double step = w / (2 * 4);
double x = 0.0;
double v_1 = -1.0;
double v_2 = 0.0;
double swap;
printf("x\tV2\tV1\tstep\n");
while ( v_2 - v_1 > 0.1 ) {
while ( v_2 > v_1 ) {
x = x + step;
v_1 = v_2;
v_2 = x * (w - x - x) * (d - x - x);
printf("%.3lf\t%.2lf\t%.2lf\t%.4lf\n", x, v_2, v_1, step);
}
step = step * -0.5;
swap = v_2;
v_2 = v_1;
v_1 = swap;
}
return EXIT_SUCCESS;
}
Output:
x V2 V1 step 1.500 121.50 0.00 1.5000 3.000 108.00 121.50 1.5000 2.250 126.56 121.50 -0.7500 1.500 121.50 126.56 -0.7500 1.875 127.62 126.56 0.3750 2.250 126.56 127.62 0.3750 2.062 127.91 127.62 -0.1875 1.875 127.62 127.91 -0.1875 1.969 127.98 127.91 0.0938 2.062 127.91 127.98 0.0938
V = h * b * d
V = x * (12 - x - x) * (12 - x - x)
V = x * (12 - 2x) * (12 - 2x)
V = 144x - 24x² - 24x² + 4x³
V = 4x³ - 48x² + 144x
Nu er formlen reduceret så meget man kan. Det er en tredjegradsligning. Du har printet, klippet og foldet 3 kasser, og nu kan vi så regne deres volume ud.
| Tern | Vol | Regnestykke | Mellemregning |
|---|---|---|---|
| 1 | 100 | 4*1³ - 48*1² + 144*1 | 4*1 - 48*1 + 144*1 |
| 2 | 128 | 4*2³ - 48*2² + 144*2 | 4*8 - 48*4 + 144*2 |
| 3 | 108 | 4*3³ - 48*3² + 144*3 | 4*27 - 48*9 + 144*3 |
Det ser ud til at man får det største volume ved 2 tern, men det kan være at 1.5 tern måske giver et større volume. Enten skal vi prøve med alle de tal der er imellem disse tal, ellers skal vi regne ud præcist hvor mange tern der er optimalt at klippe ind i arket.
Prøv først at regne det ud en masse gange. Til det formål er det nemmest med et regneark, såsom OpenOffice Calc, Excel eller Google's regneark. Formlen man skal taste ind i regnearket ser en anelse anderledes ud: =4*A2^3 - 48*A2^2 + 144*A2 , men det er det samme som førnævnte formel hvor X er blevet erstattet af A2. Ved at lave en talrække i første kolonne med 0.1 tern imellem hver linje, kan man afprøve hvor mange tern det er optimalt at klippe ind i arket. Herunder ses det at ved 1 tern, så bliver volumen 100 tern³.
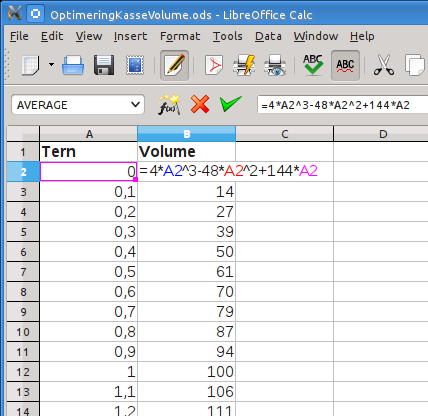
Formlen for udregning af volumen er en tredjegradsligning. Det optimale volume er det hvor toppunktet er.
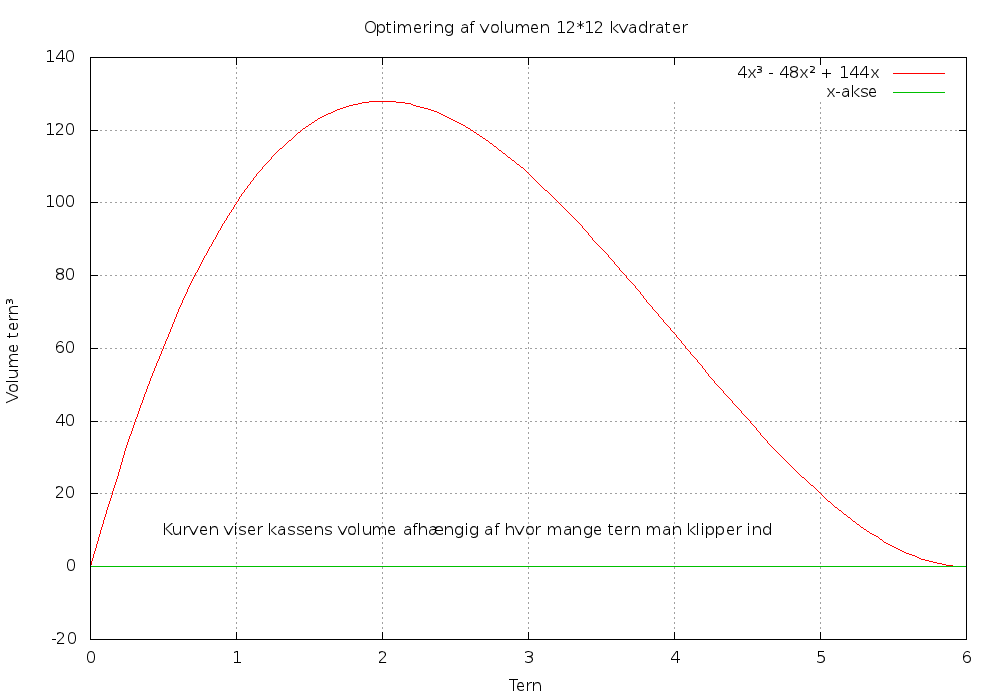
Gnuplot af tredjegradsligning.gp. Denne graf viser tredjegradsligningen 4x³ - 48x² + 144x. Det er tydeligt at toppunktet er ved 2 tern. Vi kan ikke simpelt løse tredjegradsligingen, så vi finder toppunktet, og dermed hvor mange tern ind vi skal klippe.
Hvis man differentiere en tredjegradsligning får man en andengradsligning, og det er det som gøres herunder.
V = 4x³ - 48x² + 144x
V' = 12x² - 96x + 144
Der bruges én differentieringsregel i denne formel, som er hentet fra Wikipedia, Differentialregning:
Formlen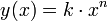 
giver den aflede 
.
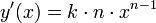Eksempel: y(x) = 4x³ => y'(x) = 4*3x³⁻¹ => y'(x) = 12x²
Gnuplot af tredje+andengradsligning.gp. Her ses igen tredjegradsligningen, men nu også den differentierede andengradsligning (blå). V' = 12x² - 96x + 144. Når man differentiere får man en ny graf, hvor alle toppunkterne fra første graf går igennem x-aksen. Den blå andengradsligning skærer altså x-aksen ved 2, og det er lige præcis der hvor toppunktet er.
En andengradsligning, altså denne parabel, kan enten skære x-aksen 0, 1 eller 2 gange. Her ses at den skærer x-aksen 2 gange. I formlen for andengradslgingen indgår dette sære '±' tegn, og det er altså kun den ene af de værdier vi får fra andengradsligning-formlen der kan bruges.
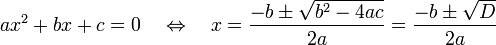
Hvis så indsætter tallenede for vores andengradsligning, får vi to resultater:
2 = (96 - sqrt(96^2 - 4*12*144)) / (2*12)
6 = (96 + sqrt(96^2 - 4*12*144)) / (2*12)
Resultatet er: 2 tern
Det sidste resultat '6' duer ikke, for hvis man klipper 6 tern ind på papiret der måler 12 tern, så får man et volume på 0.
Hjemmeopgave: Find det optimale volume af et A4 ark. Formlen 'h*b*d' bliver så i centimeter 'h*(30 - h - h)*(21 - h - h).
Denne opgave er inspireret af frividen.dk -> Matematik -> Differentialregning -> Optimering , og var oprindeligt beregnet for mindre børn, som under vejledning kan taste tallene ind på lommeregner. Nu er denne side så blevet udvidet med differentialregning og andengradsligninger.
Powered by: Qcad, Gnuplot, LibreOffice, Wikipedia, Linux, Apache, Hans Schou